모노산달로스의 행보
[Machine Learning] 다항식 선형 회귀(Multiple Linear Regression) 본문
[Machine Learning] 다항식 선형 회귀(Multiple Linear Regression)
모노산달로스 2024. 7. 18. 14:34MachineLearning - 다항식 선형 회귀

머신러닝은 데이터를 분석하고 패턴을 학습하여 자동으로 예측하거나 결정을 내리는 기술입니다. 다양한 산업에서 효율성을 극대화하고 혁신을 촉진하기 때문에 머신러닝은 현재 주목받는 기술입니다. 이러한 상황에서 미래 기술 발전의 핵심 역량을 갖추기 위해서 머신러닝의 공부는 필수적입니다.
다항식 선형 회귀 모델 (Polynomial Linear Regression Model)

다항식 선형 회귀 모델이란 다중 선형 회귀와 비슷한 면이 있습니다. 여러 개 변수의 영향을 받는 식의 형태를 가집니다. 하지만 같은 변수의 다른 거듭제곱으로 식이 표현된다는 것이 큰 특징입니다. 주로 질병의 확산이나 대출 이자와 같이 비 선형적으로 증가하는 데이터 셋을 분석하는 경우에 사용합니다.
즉, 쉽게 말해서 비선형적인 데이터를 분석하는 모델입니다. 그렇다면 왜 다항식 선형 회귀라고 불릴까요? 종속 변수 y와 독립 변수 x는 비선형 관계를 가집니다. 하지만 각 계수들은 선형 조합을 가지고 함수를 표현할 수 있습니다. 이때, 회귀 구축 시 목표는 계수의 값을 찾아서 x를 통해 y를 예측 가능하게 만드는 것입니다. 따라서, 다항식 선형 회귀는 이름 그대로 독립 변수의 다항식을 사용하지만, 회귀 계수들이 선형적으로 결합된다는 점에서 선형 회귀로 불리는 것입니다.
비선형적 데이터 예측(Non-Linear Data Prediction)
| 직군(Position) | 단계(Level) | 봉급(Salary) |
| 비즈니스 분석가(Business Analyst) | 1 | 45000 |
| 주니어 컨선턴트(Junior Consultant) | 2 | 50000 |
| 시니어 컨설턴트(Senior Consultant) | 3 | 60000 |
| 매니저(Manager) | 4 | 80000 |
| 국가 매니저(Country Manager) | 5 | 110000 |
| 지역 매니저(Region Manager) | 6 | 150000 |
| 파트너(Partner) | 7 | 200000 |
| 시니어 파트너(Senior Partner) | 8 | 300000 |
| 최고경영진(C-level) | 9 | 500000 |
| 최고경영자(CEO) | 10 | 1000000 |
만약 당신이 A 회사의 HR에서 근무한다고 가정합시다. 이번에 B 회사에서 이적하는 직원 K와 봉급 논의를 하는 상황입니다. K는 160000$를 받기를 원한다고 합니다. 그 이유를 물어보니, 자신이 이전 회사에서 그렇게 받았다고 이야기합니다. 해당 직원의 이력서를 살펴보니, 그가 지역 매니저로 2년 정도 근무했다는 사실을 알 수 있었습니다.
이러한 상황에서 우리는 위와 같은 B 회사의 봉급 표를 가지고 있습니다. 그렇다면 그의 이야기가 진실인지 허풍인지 알 수 있을까요? 이를 위해서 우리는 다항식 선형 회귀 모델을 사용해 볼 수 있습니다.
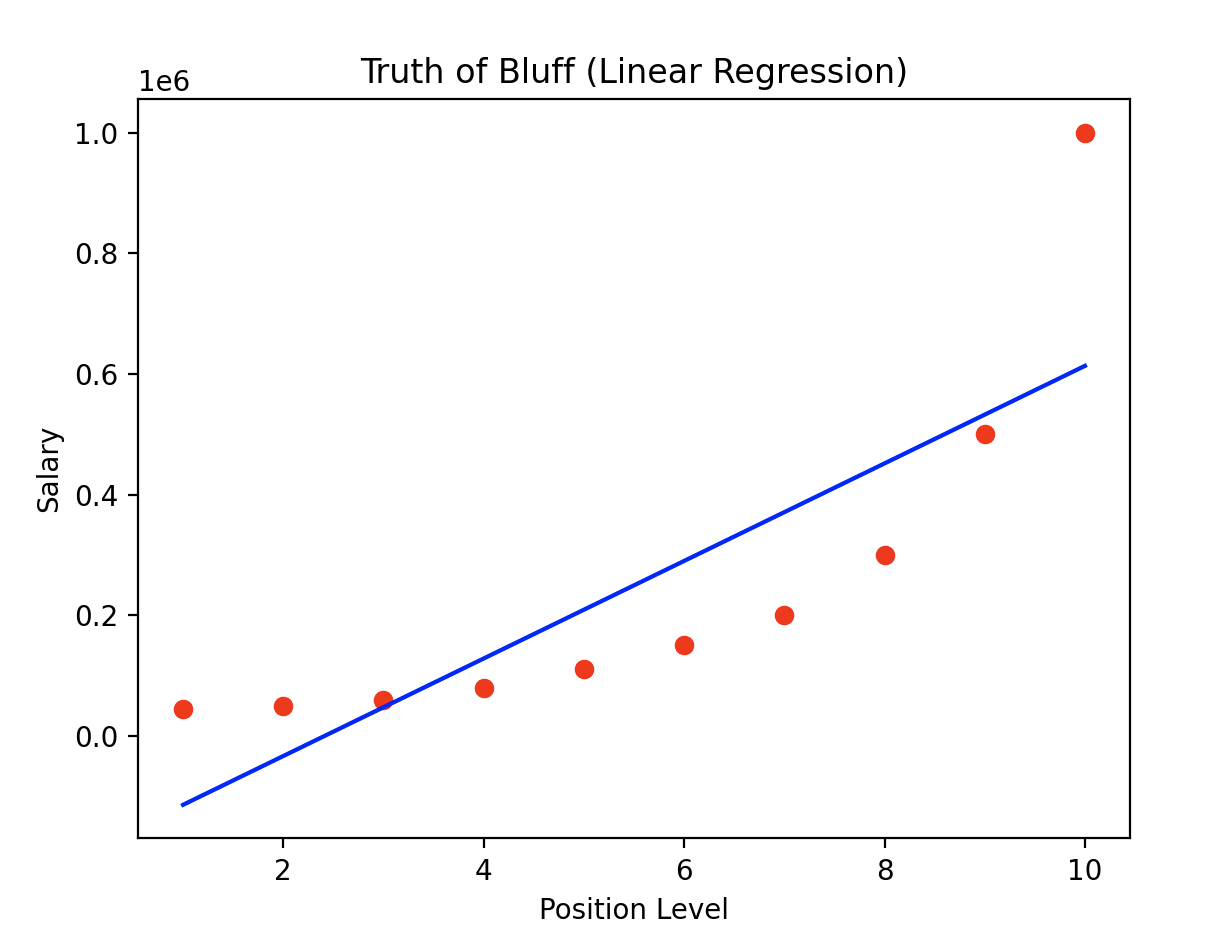
먼저 단순 선형 회귀 모델을 사용한 경우입니다. 빨간 점으로 표시된 것이 봉급표의 값이고 파란 선은 단순 선형 회귀로 예측한 결과를 나타냅니다.
보다시피 예측 값과 실제 값의 차이가 매우 크게 나타나는 것을 확인할 수 있습니다. 즉, 해당 데이터에 단순 선형 회귀 모델은 적절하지 않다는 것을 눈으로 확인 가능합니다.
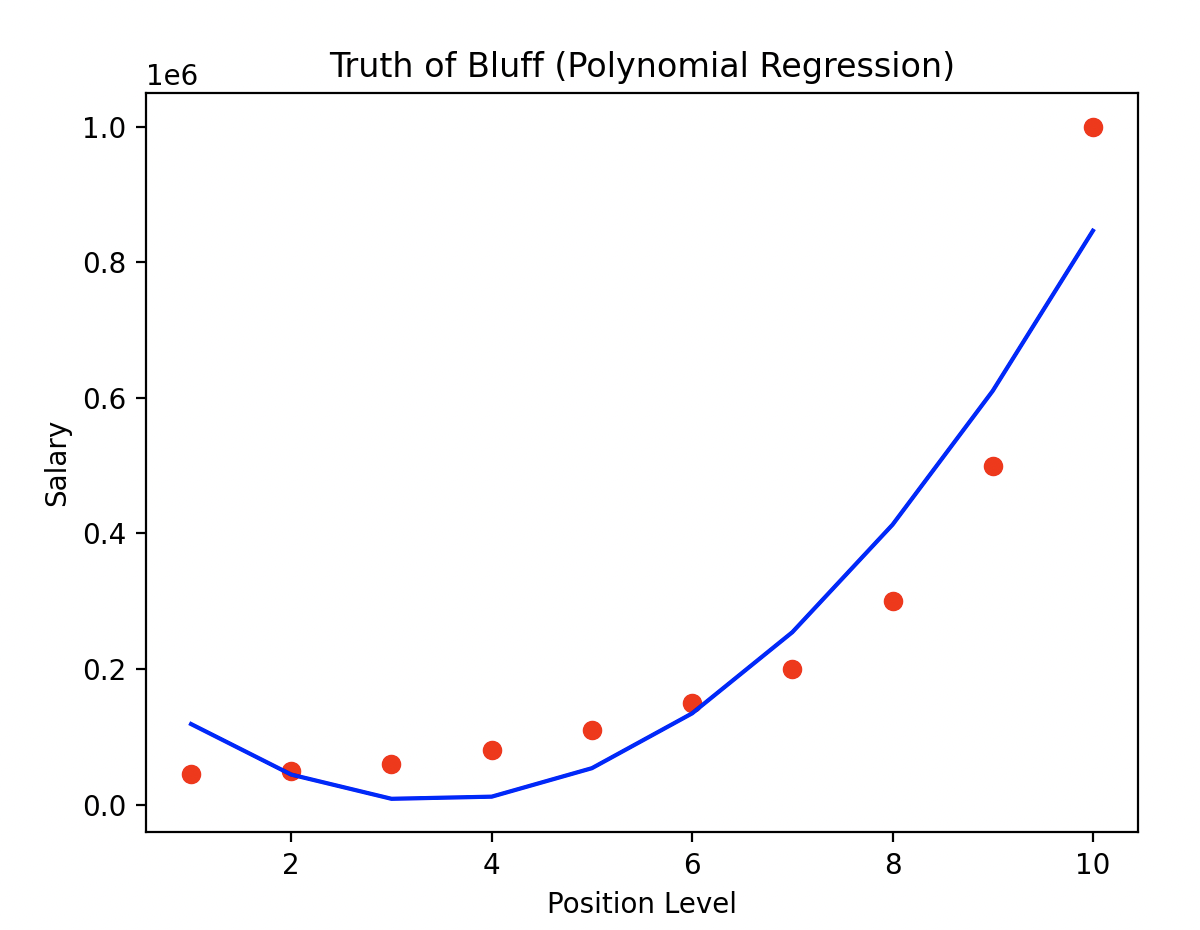
이번에는 차수가 2인 다항식 선형 회귀 모델을 사용한 결과입니다. 앞서 확인한 모델과 다르게 예측 값이 실제 값에 근접한다는 것을 확인할 수 있습니다. 예측선이 직선이 아닌 곡선으로 표현되기 때문에 비선형적 데이터를 분석하기에 적절합니다.
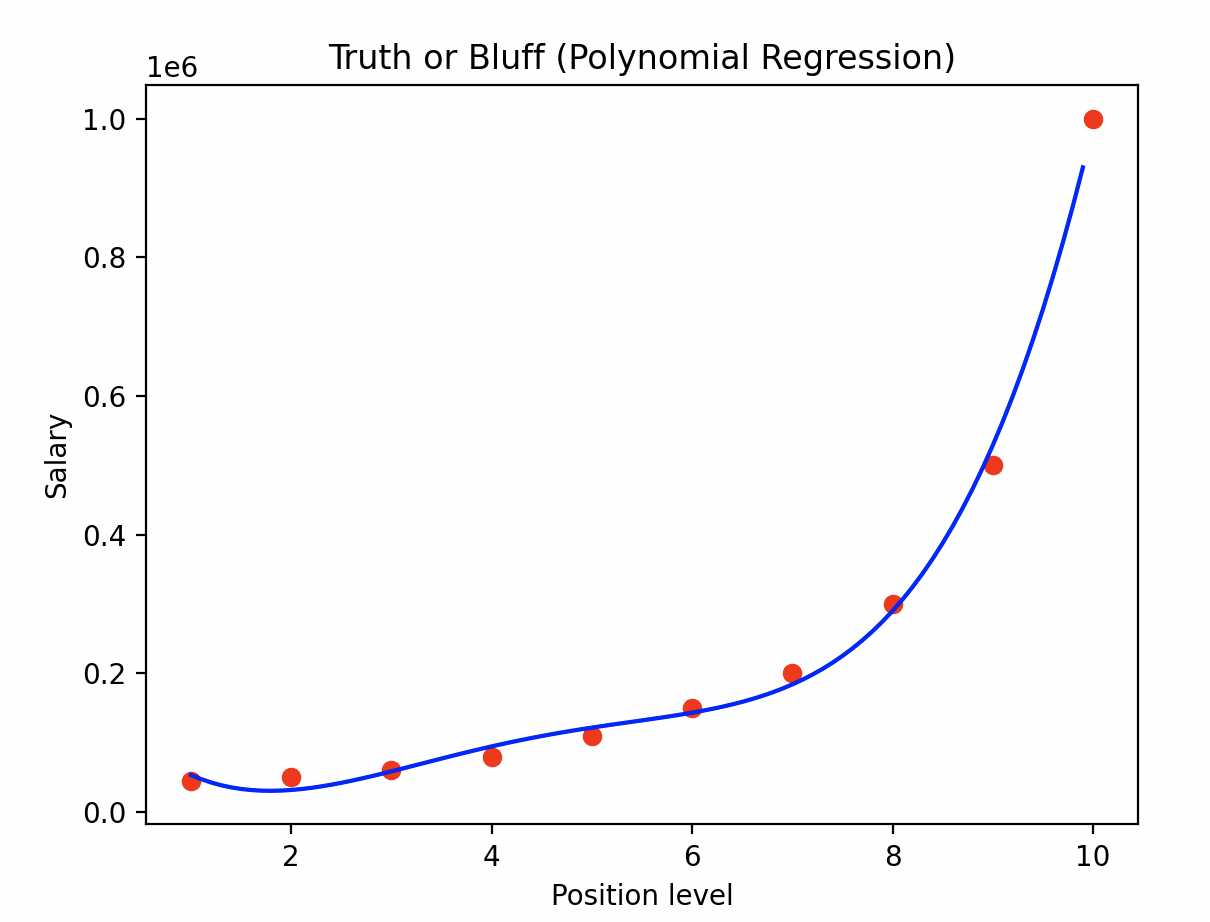
이번에는 차수가 4인 다항식 선형 회귀 모델을 사용한 결과입니다. 차수가 증가하니 더욱 정확한 결과 값을 보여주고 있습니다. 그렇다면 여기서 의문이 생깁니다. 어떠한 차수의 값이 적절한지 확인하는 방법이 있을까요?
방정식에서 올바른 차수(The right degree of the equation)
다항식 선형 회귀 모델에서 차수의 값이 증가하면 모델의 성능 또한 증가하게 됩니다. 하지만 그와 동시에 과대적합(Overfitting) 혹은 과소적합(Underfitting)의 위험성도 증가하게 됩니다. 차수를 찾는 방법은 두 가지가 존재합니다.
1. 전진 선택법 : 가장 적절한 모델이 정의될 때까지 차수를 증가시켜 나갑니다.
2. 후진 선택법 : 가장 적절한 모델이 정의될 때까지 차수를 감소시켜 나갑니다.
Ref.
Understanding Polynomial Regression!!!
Polynomial Regression is a special case of Linear Regression where we fit the polynomial equation on the data with a curvilinear…
medium.com
'AI > MachineLearning' 카테고리의 다른 글
| [Machine Learning] 다중 선형 회귀(Multiple Linear Regression) (0) | 2024.07.11 |
|---|---|
| [Machine Learning] 단순 선형 회귀(Simple Linear Regression) (0) | 2024.07.09 |
| [Machine Learning] 데이터 전처리 과정, 데이터 셋 분리하기, 특성 스케일링(Data Preprocessing) (0) | 2024.07.04 |



