[Linear Algebra] 가우스-조던 소거법 (Gauss-Jordan elimination)

선형대수학 - 가우스 조던 소거법

 

선형 대수학의 아버지 윌리엄 로월 해밀턴

 

인공지능 시대가 떠올랐습니다. 선형대수학은 데이터의 표현과 변환에 핵심적인 역할을 하여 AI 모델의 학습 및 예측 과정에서 효율적인 계산을 가능하게 합니다. 또한, 차원 축소와 같은 기법으로 고차원 데이터를 효과적으로 처리하고 시각화하므로 AI 개발을 위해 선형대수학 공부가 필수적입니다.

 

위와 같은 이유로 선형대수학을 공부하면서 정리한 내용을 담은 포스트입니다.

---

가우스 조던 소거법(Gauss-Jordan elimination)이란?

우리는 행렬을 기약 행 사다리꼴(Reduced row-echelon form)의 형태로 표현하는 것이 방정식 풀이에 도움을 준다는 것을 배웠습니다. 행렬의 행 연산을 통해서 이것을 수행하는데, 가우스 조던 소거법(Gauss-Jordan elimination)이란 그러한 변환을 단계별로 표현한 알고리즘입니다.

 

1. (선택사항) 행렬의 행에서 상수 배가 있는 경우 인수를 꺼내서 간단하게 만들어줍니다.
2. 만약 피벗이 0이라면 다른 행과 위치를 바꾸어줍니다.
3. 0이 아닌 피벗을 1로 만들어줍니다.
4. 피벗 열의 다른 수를 0으로 만들어줍니다.
5. 2번으로 돌아가서 반복합니다.

 

가우스 조던 소거법은 위와 같은 방법으로 수행이 가능합니다. 위의 5가지 단계를 잘 기억한다면 소거법을 문제없이 진행할 수 있습니다.

 

 

---

 

 

 

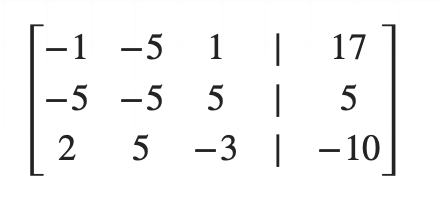
예시를 통해서 소거법이 실제로 어떻게 사용이 되는지 알아보겠습니다. 위와 같은 행렬을 기약 행 사다리꼴의 형태로 변환하겠습니다. 먼저 첫 번째 행에 대하여 소거법을 수행합니다.

 

가우스 조던 소거법의 첫 번째 단계, '행렬의 행에서 상수 배가 있는 경우 인수를 꺼내서 간단하게 만들어줍니다.'를 수행합니다. 따라서, 두 번째 행을 5로 나누어줍니다.

 

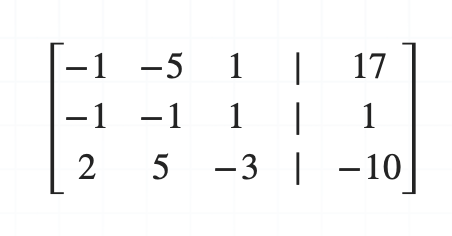
가우스 조던 소거법의 두 번째 단계, '만약 행의 피벗이 0이라면 다른 행과 위치를 바꾸어줍니다.'를 수행합니다. 이미 -1로 0이 아니므로 이 단계는 넘어갑니다.

 

가우스 조던 소거법의 세 번째 단계, '0이 아닌 피벗을 1로 만들어줍니다.'를 수행합니다. 첫 번째 행에 -1을 곱하여 피벗을 1로 만들어줍니다.

 

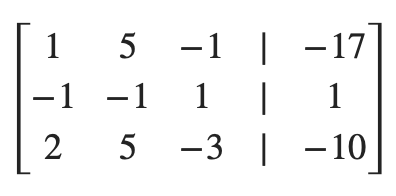
가우스 조던 소거법의 네 번째 단계, '피벗 열의 다른 수를 0으로 만들어줍니다.'를 수행합니다. 따라서, 첫 번째 행과 두 번째 행을 더합니다.

 

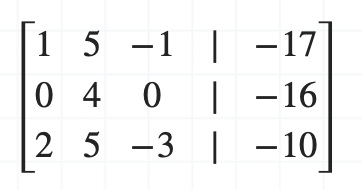
피벗 열의 세 번째 행인 2 또한 0으로 바꾸어주어야 합니다. 따라서 첫 번째 행에 -2를 곱한 뒤 세 번째 행과 더해줍니다.

 

이제 첫 번째 열은 1, 0, 0과 같은 형태가 되었습니다. 이제 두 번째 단계로 돌아가서 두 번째 행에 대해 앞서 수행한 연산을 반복합니다.

 

가우스 조던 소거법의 두 번째 단계, '만약 행의 피벗이 0이라면 다른 행과 위치를 바꾸어줍니다.'를 수행합니다. 이미 4로 0이 아니므로 이 단계는 넘어갑니다.

 

가우스 조던 소거법의 세 번째 단계, '0이 아닌 피벗을 1로 만들어줍니다.'를 수행합니다. 두 번째 행에 4를 나누어 피벗을 1로 만들어줍니다.

 

가우스 조던 소거법의 네 번째 단계, '피벗 열의 다른 수를 0으로 만들어줍니다.'를 수행합니다. 따라서, 두 번째 행에 -5를 곱한 뒤 첫 번째 행과 더해줍니다.

 

 

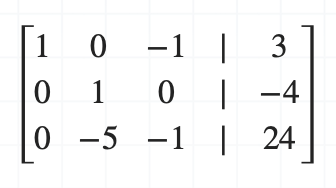
세 번째 행에 대해서도 연산을 수행합니다. 두 번째 행에 5를 곱한 뒤 세 번째 행과 더해줍니다.

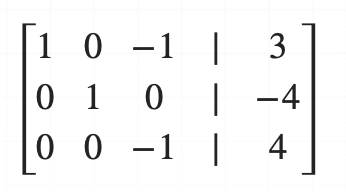
이제 두 번째 열은 0, 1, 0 과 같은 형태가 되었습니다. 이제 두 번째 단계로 돌아가서 세 번째 행에 대해 앞서 수행한 연산을 반복합니다.

 

가우스 조던 소거법의 두 번째 단계, '만약 행의 피벗이 0이라면 다른 행과 위치를 바꾸어줍니다.'를 수행합니다. 이미 -1로 0이 아니므로 이 단계는 넘어갑니다.

 

가우스 조던 소거법의 세 번째 단계, '0이 아닌 피벗을 1로 만들어줍니다.'를 수행합니다. 두 번째 행에 -1을 곱하여 피벗을 1로 만들어줍니다.

가우스 조던 소거법의 네 번째 단계, '피벗 열의 다른 수를 0으로 만들어줍니다.'를 수행합니다. 따라서, 세 번째 행과 첫 번째 행을 더합니다.

 

 

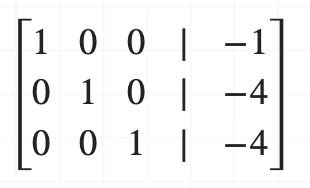
그 결과 행렬이 기약 행 사다리꼴 형태가 되었습니다. 방정식을 풀면 (x, y, z) = (-1, -4, -4)가 됩니다.

---